Contextualized Classification

Contextual models allow to identify heterogeneous effects which change between different contexts. The contextualized package provides easy access to these heterogeneous models through the contextualized.easy module interfaces. This notebook shows a simple example of using contextualized.easy classification.

1. Generate Simulation Data

In this simulated classification, we’ll study the simple varying-coefficients case where \(\text{logit}(Y) = X\beta(C) + \epsilon\), with \(\beta(C) \sim \text{N}(C\phi, \text{I})\), and \(\epsilon \sim \text{N}(0, 0.01 \text{I})\)

import numpy as np
n_samples = 200
n_context = 1
n_observed = 1
n_outcomes = 3
C = np.random.uniform(-1, 1, size=(n_samples, n_context))
X = np.random.uniform(-1, 1, size=(n_samples, n_observed))
phi = np.random.uniform(-10, 10, size=(n_context, n_observed, n_outcomes))
beta = np.tensordot(C, phi, axes=1) + np.random.normal(0, 0.01, size=(n_samples, n_observed, n_outcomes))
Y = np.array([np.tensordot(X[i], beta[i], axes=1) for i in range(n_samples)])
Y_prob = 1. / (1+np.exp(-Y))
Y = np.random.uniform(0, 1, size=(n_samples, n_outcomes)) < Y_prob

2. Build and fit model

Uses an sklearn-type wrapper interface.

%%capture
from contextualized.easy import ContextualizedClassifier
model = ContextualizedClassifier(alpha=1e-3, l1_ratio=0.0, n_bootstraps=3)
model.fit(C, X, Y, max_epochs=100,  learning_rate=1e-3)

3. Inspect the model predictions.

%%capture
preds = model.predict(C, X)[:, 0] # predicted labels
probs = model.predict_proba(C, X)[:, 0, 1] # predicted probabilities

import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams.update({'font.size': 18})

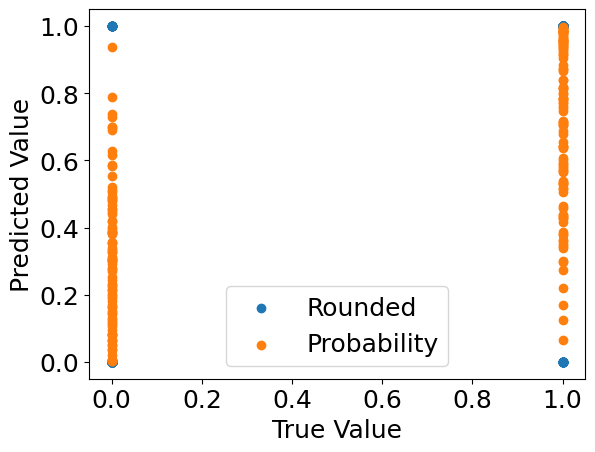
plt.scatter(Y[:, 0], preds, label='Rounded')
plt.scatter(Y[:, 0], probs, label='Probability')
plt.xlabel("True Value")
plt.ylabel("Predicted Value")
plt.legend()
plt.show()

4. Check what the individual bootstrap models learned.

%%capture
model_preds = model.predict(C, X, individual_preds=True)
# predict() automatically rounds the predictions for classifiers.
# If you want probabilities, use predict_proba()

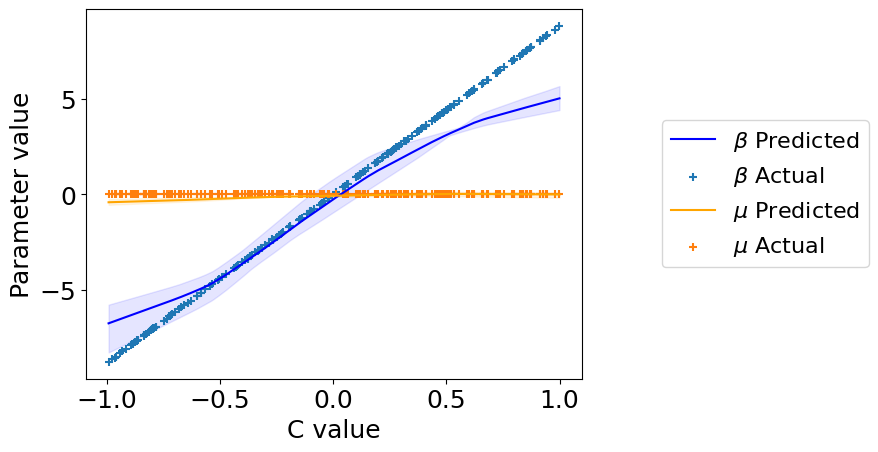
5. Check what parameters the models learned.

%%capture
beta_preds, mu_preds = model.predict_params(C, individual_preds=True)
beta_preds.shape  # (n_bootstraps, n_samples, n_outcomes, n_predictors)
mu_preds.shape  # (n_bootstraps, n_samples, n_outcomes)

order = np.argsort(C.squeeze())  # put C in order for plotting
C = C[order].squeeze()
beta_preds = beta_preds[:, order]
mu_preds = mu_preds[:, order]
beta = beta[order]

plt.plot(
    C, np.mean(beta_preds[:, :, 0], axis=0),
            label='$\\beta$ Predicted', color='blue')
plt.fill_between(
    C,
    np.percentile(beta_preds[:, :, 0], 2.5, axis=0).squeeze(),
    np.percentile(beta_preds[:, :, 0], 97.5, axis=0).squeeze(),
    color='blue', alpha=0.1
)
plt.scatter(C, beta[:, :, 0], label='$\\beta$ Actual', marker='+')

plt.plot(
    C, np.mean(mu_preds[:, :, 0], axis=0),
            label='$\\mu$ Predicted', color='orange')
plt.fill_between(
    C,
    np.percentile(mu_preds[:, :, 0], 2.5, axis=0).squeeze(),
    np.percentile(mu_preds[:, :, 0], 97.5, axis=0).squeeze(),
    color='orange', alpha=0.1
)
plt.scatter(C, np.zeros_like(C), label='$\\mu$ Actual', marker='+')
plt.legend(loc='center right', bbox_to_anchor=(1.6, 0.5), fontsize=16)
plt.xlabel("C value")
plt.ylabel("Parameter value")
plt.show()